On the Flexibility of Parametric Spectral Filters

This year I published Parametric Spectral Filters for Fast Converging, Scalable Convolutional Neural Networks in ICASSP. In the conclusions section I point out several future directions to continue the line of exploration of spectral domain convolutional neural nets. The most irking question to me personally was: Exactly how flexible are parametric spectral filters?

Parametric spectral filters have an extremely constrained search space in which they are permitted to learn their filters. Due to this, it is highly probably that the optimal filter for a given task is unlearnable by a parametric spectral filter. That being said, how far off of the perfect filter will the learned filter be? Yesterday I performed some brief analysis to begin answering that question.

First Experiment

This Experiment is Open Source.

Auto-encoders are an excellent flexibility benchmark. If the encoder network is unable to capture an important piece of information, perhaps due to lack of flexibility in filter space, the results will very obviously show this. This experiment uses mnist as the dataset. I made this choice to perform fast prototyping.

First, I create a spatial domain benchmark autoencoder:

def create_model():
  input = layers.Input(shape=(28, 28, 1))
  # Encoder
  x = layers.Conv2D(32, (3, 3), activation="relu", padding="same")(input)
  x = layers.MaxPooling2D((2, 2), padding="same")(x)
  x = layers.Conv2D(32, (3, 3), activation="relu", padding="same")(x)
  x = layers.MaxPooling2D((2, 2), padding="same")(x)

  # Decoder
  x = layers.Conv2DTranspose(32, (3, 3), strides=2, activation="relu", padding="same")(x)
  x = layers.Conv2DTranspose(32, (3, 3), strides=2, activation="relu", padding="same")(x)
  x = layers.Conv2D(1, (3, 3), activation="sigmoid", padding="same")(x)
  x = layers.Reshape((28, 28))(x)
  # Autoencoder
  autoencoder = Model(input, x)
  autoencoder.compile(optimizer="adam", loss="binary_crossentropy")
  return autoencoder

Upon converging, the spatial domain autoencoder scores the following loss:

loss: 0.0627 - val_loss: 0.0623

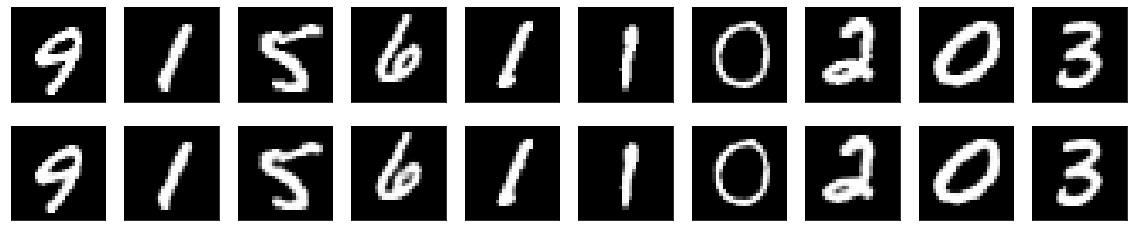
This will serve as our baseline.

Next I create an autoencoder with a spectral encoder and a spatial decoder. I still use spatial domain downsampling in order to ensure that any difference in performance between the two networks is due to the spectral filters.

from spectral_neural_nets.layers import Gaussian2DFourierLayer, fft_layer, from_complex, to_complex, ifft_layer

def spectral_block(x):
  x = fft_layer(x)
  x = from_complex(x)
  x = Gaussian2DFourierLayer(32)(x)
  x = layers.Activation('relu')(x)
  x = to_complex(x)
  x = ifft_layer(x)
  x = layers.MaxPooling2D((2, 2), padding="same")(x)
  return x

def create_spectral_model():
  input = layers.Input(shape=(28, 28))
  x = layers.Reshape((28, 28, 1))(input)

  # Encoder
  x = spectral_block(x)
  x = spectral_block(x)
  # Decoder
  x = layers.Conv2DTranspose(32, (3, 3), strides=2, activation="relu", padding="same")(x)
  x = layers.Conv2DTranspose(32, (3, 3), strides=2, activation="relu", padding="same")(x)
  x = layers.Conv2D(1, (3, 3), activation="sigmoid", padding="same")(x)
  x = layers.Reshape((28, 28))(x)
  # Autoencoder
  autoencoder = Model(input, x)
  autoencoder.compile(optimizer="adam", loss="binary_crossentropy")
  return autoencoder

Upon converging, the spectral encoder/spatial decoder autoencoder scores the following loss:

loss: 0.0816 - val_loss: 0.0809

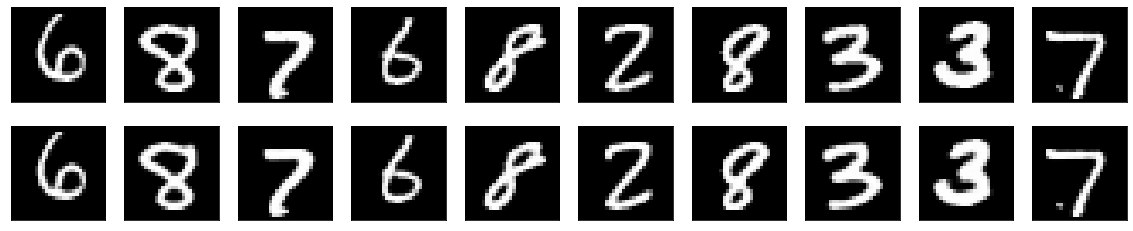
Conclusion

This experiment shows us two things:

• parametric spectral filters are sufficiently flexible to extract key information from an image to perform autoencoding
• 2D Gaussian parametric spectral filters are less flexible than traditional CNNs

This leads me to want to explore two future directions:

• Using this experiment structure, I'd like to explore the flexibility of a wide array of parametric functions
• I'd like to perform end to end spectral domain autoencoding.

The latter will be my next experiment

My Next Experiment

Unfortunately, I cannot yet perform end to end autoencoding in the spectral domain. End to end autoencoding requires a convolutional layer that supports striding. I have not quite worked out the details as to how this will work with spectral domain cnn layers. Next week, I will be taking a stab at this and hope to perform end to end autoencoding in the spectral domain. Should the filters succeed at autoencoding, there will be a strong argument to be made that parametric spectral filters are sufficiently flexible. If they are not able to effectively autoencode, I will try a more flexible parametric function.